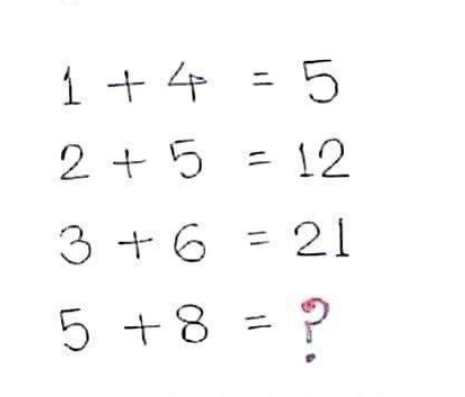🔍 Décoder l’énigme mathématique virale : le modèle caché derrière une addition qui n’en est pas une

Introduction

Depuis quelques années, un casse-tête mathématique a envahi les réseaux sociaux, les groupes de discussion et les plateformes éducatives. Présentée comme une série d’additions simples, cette énigme déstabilise et intrigue même les esprits les plus logiques. Pourquoi ? Parce que les résultats affichés semblent aller à l’encontre de toutes les règles fondamentales de l’arithmétique. Pourtant, sous cette apparente absurdité se cache une structure logique ingénieuse, voire élégante.

Voici le casse-tête tel qu’il apparaît généralement :

1 + 4 = 5  
2 + 5 = 12  
3 + 6 = 21  
5 + 8 = ?

La dernière équation fait appel à votre capacité de raisonnement logique, votre attention aux détails et votre volonté de remettre en question vos réflexes mathématiques les plus élémentaires.

---

Partie 1 : Pourquoi ce casse-tête perturbe autant de gens

Dès qu’on lit les premières lignes, une alarme mentale se déclenche. La première opération est correcte (1 + 4 = 5), mais les suivantes posent problème :

• 2 + 5 = 12 ❌
• 3 + 6 = 21 ❌

Vous pensez : “Attendez, 2 + 5 = 7, pas 12.” Vous avez raison… si l’on suit une logique arithmétique classique. Mais ici, l’objectif est différent : il s’agit de trouver le modèle caché, la structure logique derrière ces résultats inattendus.

Ce n’est pas un problème de calcul, mais une invitation à penser autrement.

---

Partie 2 : La logique cumulative – Une solution populaire

Examinons de près les opérations une à une, en adoptant une approche dite cumulative :

Ligne 1 :

1 + 4 = 5 ✅

Simple addition. Pas de souci ici.

Ligne 2 :

2 + 5 = 7  
+ résultat précédent (5)  
= 12 ✅

Ligne 3 :

3 + 6 = 9  
+ résultat précédent (12)  
= 21 ✅

Ligne 4 :

5 + 8 = 13  
+ résultat précédent (21)  
= 34 ✅

✔️ Réponse selon cette méthode : 34

---

Partie 3 : Décomposition détaillée du raisonnement cumulatif

Ligne	Opération de base	Résultat brut	Résultat précédent	Total final
1	1 + 4	5	–	5
2	2 + 5	7	5	12
3	3 + 6	9	12	21
4	5 + 8	13	21	34

La logique ici repose sur une accumulation des résultats précédents. Chaque nouvelle ligne dépend du résultat obtenu dans la ligne précédente. C’est une sorte de progression additive.

---

Partie 4 : Une autre approche – l’addition multiplicative

Et si la logique suivie n’était pas cumulative, mais plutôt une combinaison d’addition et de multiplication ?

Testons l’idée suivante :

a + b = a + (a × b)

Ligne 1 :

1 + (1 × 4) = 1 + 4 = 5 ✅

Ligne 2 :

2 + (2 × 5) = 2 + 10 = 12 ✅

Ligne 3 :

3 + (3 × 6) = 3 + 18 = 21 ✅

Ligne 4 :

5 + (5 × 8) = 5 + 40 = 45 ✅

✔️ Réponse selon cette méthode : 45

---

Partie 5 : Comparaison des deux solutions

Méthode	Résultat final
Cumulative	34
Addition + Multiplication	45

Les deux réponses sont parfaitement défendables, à condition que la logique utilisée soit cohérente du début à la fin.

---

Partie 6 : Autres interprétations possibles (moins convaincantes)

Hypothèse : a × b – a

• 1 × 4 – 1 = 3 ❌
• 2 × 5 – 2 = 8 ❌
  Rejeté.

Hypothèse : a × (b + 1)

• 1 × (4 + 1) = 5 ✅
• 2 × (5 + 1) = 12 ✅
• 3 × (6 + 1) = 21 ✅
• 5 × (8 + 1) = 45 ✅

Encore une fois, nous obtenons 45. Cela donne une troisième justification pour ce résultat. Intéressant, non ?

---

Partie 7 : Le modèle derrière le succès viral de cette énigme

Pourquoi cette énigme, en particulier, est-elle devenue virale ? Plusieurs raisons :

1. Simplicité apparente

Clique sur page 2 pour suivre